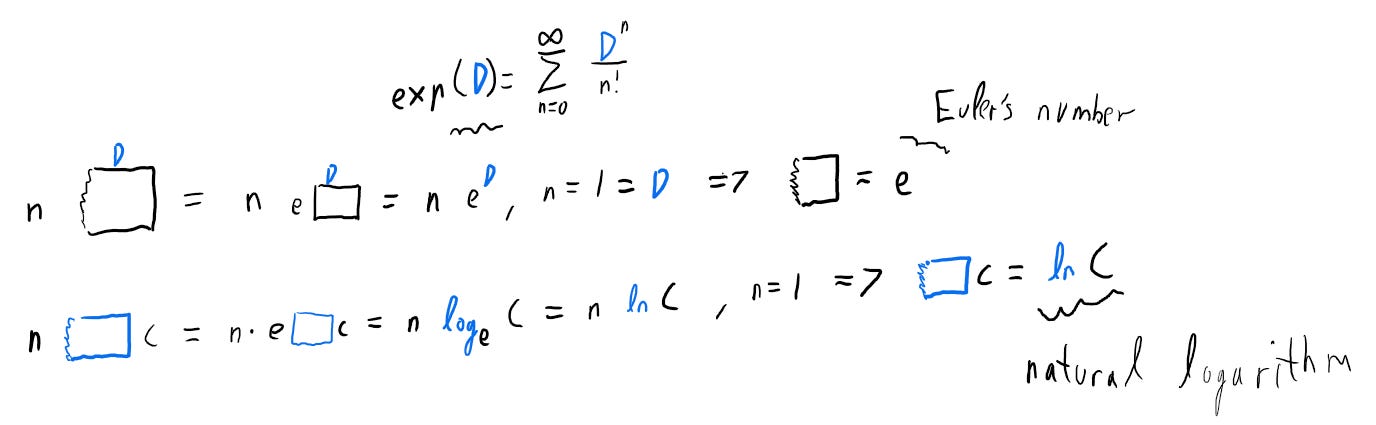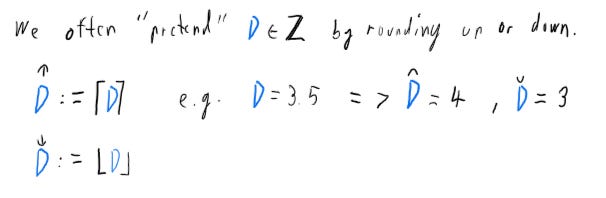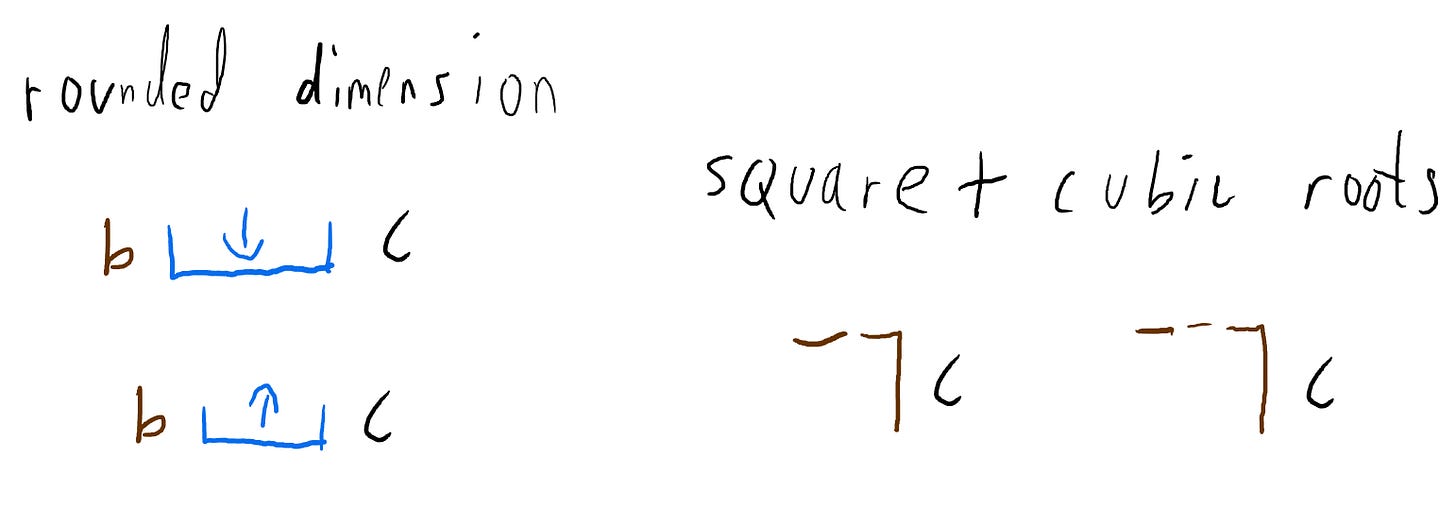Improved HyperSquare Notation Part 2: Common One-Argument Forms

And now we save even more time!

This is a follow-up post on yesterday’s improvements and the original notation post here.

One-Argument Forms

We usually just write the root-expression and by convention everyone knows, that without further argument, that we are referring to the square-root. Nothing wrong with saving time, by writing fewer numbers, but the cubic root is also quite important, so we shall implement this feature by slightly manipulating the symbol instead.

We often write logarithms, without specifying the base. In that case, the Grand Mathematicians will assume that the base is e, Dashing Computer Scientists like yours truly will assume base 2, and all of you dirty apes Salt-of-the-Earth folk will assume base 10. The impulse here is honorable as well, but in practice this leads to a lot of confusion and cognitive overhead, when switching between various numerical contexts.¹ So we shall distinguish via altering symbols, as well.

What a mess, we’ve made :(

Base 2 and Base 3

We indicate base 2 and 3 for exponentiation and logarithms by writing the left side of the square with two or three, instead of just the usual one stroke. Same idea for the square and cubic roots, except for the top-side.

Squaring and Cubing a base might as well also be here, but I forg- is left as exercise to the reader :)

Nature-based Mathematics

One of the most common and important bases is of course Euler’s number. Also known as “the natural base”.

Base e is written reminiscent to a vine, giving it the association to nature.

Nature is squiggly lines, obviously.

One advantage here, is that we free up the letter e for use as a variable.² We may speak this in the usual “e to the power of D” or as “natural base to D”. We could extend this concept to the “natural root” as well, but I don’t remember having ever seen that expression, so I left it out for now.

Creature Comfort: Rounded Logarithms

First I’m introducing a top-fix notation for the common rounding operator. The usual one follows a strange “surround-fix”-notational pattern, which I seldom find desirable.³ Also why the “rounding”-symbol of all things happens to be as angular as a Cybertruck, is one of those great mysteries, I never care to find an answer for.

New rounding Notation. Now round!

Then we apply these new rounding-operators to the Hypersquare, which allows us to conveniently express a number’s rough size with a simple whole number. Post-decimal values of the Dimension are impossible to intuitively interpret accurately anyway, so often we just ignore them.

Note that we already established that we don’t need to write out all those 10s, this is merely for clarity’s sake.

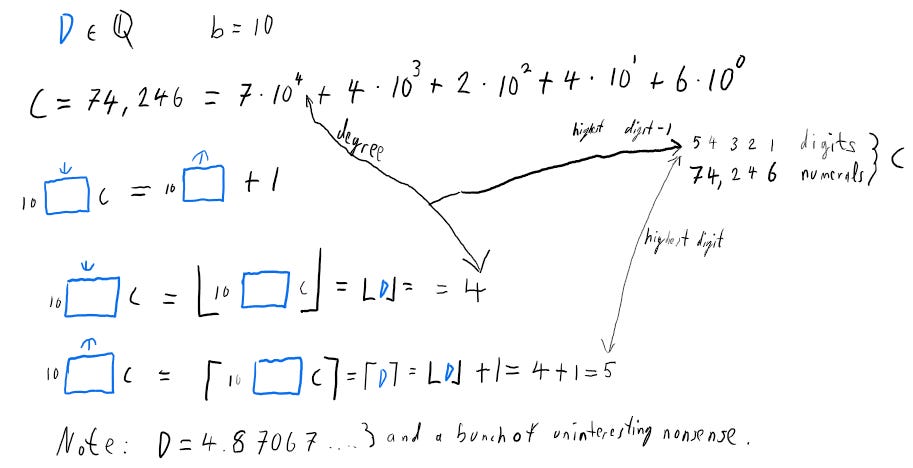
The rounded down version corresponds to the highest power, if we were to write our number C in base 10 and write it like we would a Polynomial expression. This is also referred to as the “degree” of a polynomial.

Short forms

The short form-versions of all these I find easier to read, than their long versions. Sometimes less truly is more!

Some of those may appear a bit ugly, but I blame myself and my bad handwriting.

I’ve decided to establish b, B and 𝔹 in some later posts after all, as they’re more important for the number representation-topic. I’ll leave their meaning a mystery for now :)

I blame it all on my drawing tablet :)

1. Logarithms really should not be made any more complicated than they are, hence why I normally refuse to even use the word and prefer the word “Dimension”

2. Whilst Herr Euler deserves all the glory in the world, I must insist on mathematical expressions not having references of random celebrities inserted! I’m sure he would understand.

3. Similar to the absolute value expression |-5| = 5, though for that one I’m not sure yet, how best to replace it, as it contains often larger expressions.