Triangle of Power ->Hypersquare: Replacing Symbol and Introducing Basic Geometric Interpretation
Too far?! Not far enough!
This post is about developing a more efficient notation for exponentiation, taking the root and logarithms, improving upon a famous 3b1b-video.1
Summary:
To fully understand the striking visual beauty and salient advantages of the new notation, watch the video of 3b1b on the “Triangle of Power” in full and then play with it yourself.
All the mechanics and tricks that work for the triangle of power will also work for my hypersquare. Ideally I’d make my own YouTube video or at least animations, and the 3b1b-tools are open-source now and well-documented, but I haven’t the time nor budget to replicate this sort of work for now.
In this post, I will change the triangle into a square-notation, make it more logical, extendable and color-coded on a symbolic level.
And I will also introduce a set of new parameter labels for the three operations.
In the next post, I will get into the how these operations are inadequately and misleadingly represented in the English language and develop a new set of conventions, which are better in every conceivable way.
Introduction: The Triangle of Power
And then establishes a convention that replaces three horrible symbols with one far more visually pleasing one.
But the Triangle is the Wrong Symbol!
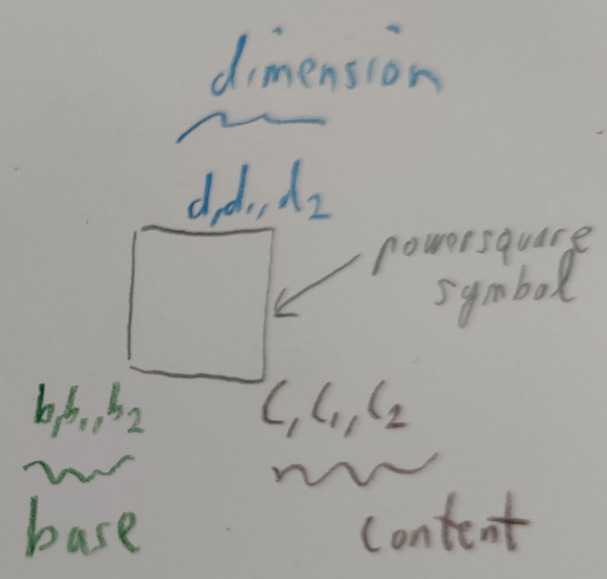
The fundamental relationship is not actually a n-dimensional triangle, but a n-dimensional hypercube (or hypersquare as I prefer to call them), which in the 2 dimensions we normally put things to paper, happens to be a square!
To understand this, study the figure below:
Why use the wrong symbol of an equilateral triangle, when you can just use the correct one and use a square instead?
Additionally, the n-dimensional squares we are actually modelling are merely one of three possible regular polytopes (those are shapes, with a constant baselength, that can be regularly extended into higher dimensions).
The other two are simplex and orthoplex, which in the 0-dimensional and 1-dimensional case look the same as the hypercube.
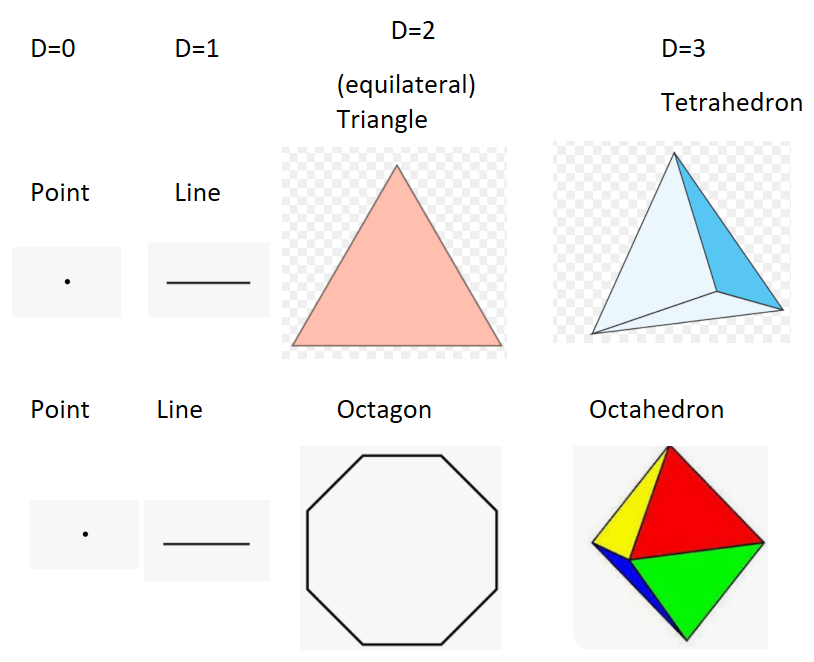
The other two regular polytopes have equivalent operations to exponentiation, roots and logarhithms. We will want to reserve the triangle symbol, as the simplex becomes an equilateral triangle in 2d.
Fixing Parameter Names
The parameter names of the three related operations are an absolute mess. E.g. the exponentiation-operation, the term power used both for the the second argument, as well as the return value. The term anti-logarithm is unnecessarily long, and it’s a wild mix of English and Latin words.
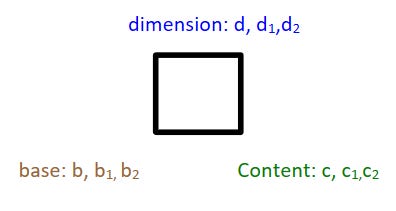
Instead of this nonsense, we cut it down to three parameter names, of which the exponentiation, nth-root and logarithm functions each take two of and return out the other as a return variable. Those parameters are exactly what exhaustively describes every possible hypersquare, relating each expression to a specific geometric object.
We hence use the triple of (base, dimension, Content). When no more words are needed, there must be no more words!
Base corresponds to the length of the base edge for a line, square or a cube.
Content corresponds to the length of a line, the area of a square or the volume of a cube. Dimension for a line is 1, square is 2 and for a cube is 3.
Color-coding arguments
Like in the last post about refactoring the trig-functions, we use the 2d-space axis visualization again.
The base-parameter will be green as we tend to label the side of a square that is parallel to the x-axis or lies thereupon as the base.
The dimension will be blue, because it will be on top of the square, therefore higher in the y-axis. The Content will be brown, as it has good contrast and no conflicting associations in 2d-space.
The symbol itself shall be named "hypersquare”.
Some Extra Mnemonics
Note that capitalization of the default-variable emphasizes that in the more comfortable and common cases, the Content has usually a larger magnitude than it’s base. E.g. square any natural number as the base and you get a Content greater-equal than itself.
This is convenient, as in physics, we usually work in whole number dimensions and Content is often assigned a higher-dimensional unit, like m² (square meters) or m³ (cubic meters) compared to the base, which will be in m (meters). Content also starts with C like its characteristic variable and which happens to be third letter in the alphabet, which makes it easy to remember as the third element in the triple (base, dimension, Content) and matches where we would place variables on the hypersquare when going left to right.
Mnemonic Properties
For faster pattern matching, we use the corresponding triple of variable names (b, d, C), when abstractly discussing the properties of these operations. When necessary, we also use the more scalable subscripts, over the common letter-incrementation (a, b, c; d, e, f; C, D, E etc.).
Of course, variable names can be freely chosen, but when we have no reason to encode meta-mathematical extra-information for a specific problem, it is better to stick with one carefully-chosen convention for recognizability. In the same vein, we also color the square itself corresponding to its return parameter.
Thank you dear friend, who pointed out that I should have lead with that and that not everyone has seen that video already :)



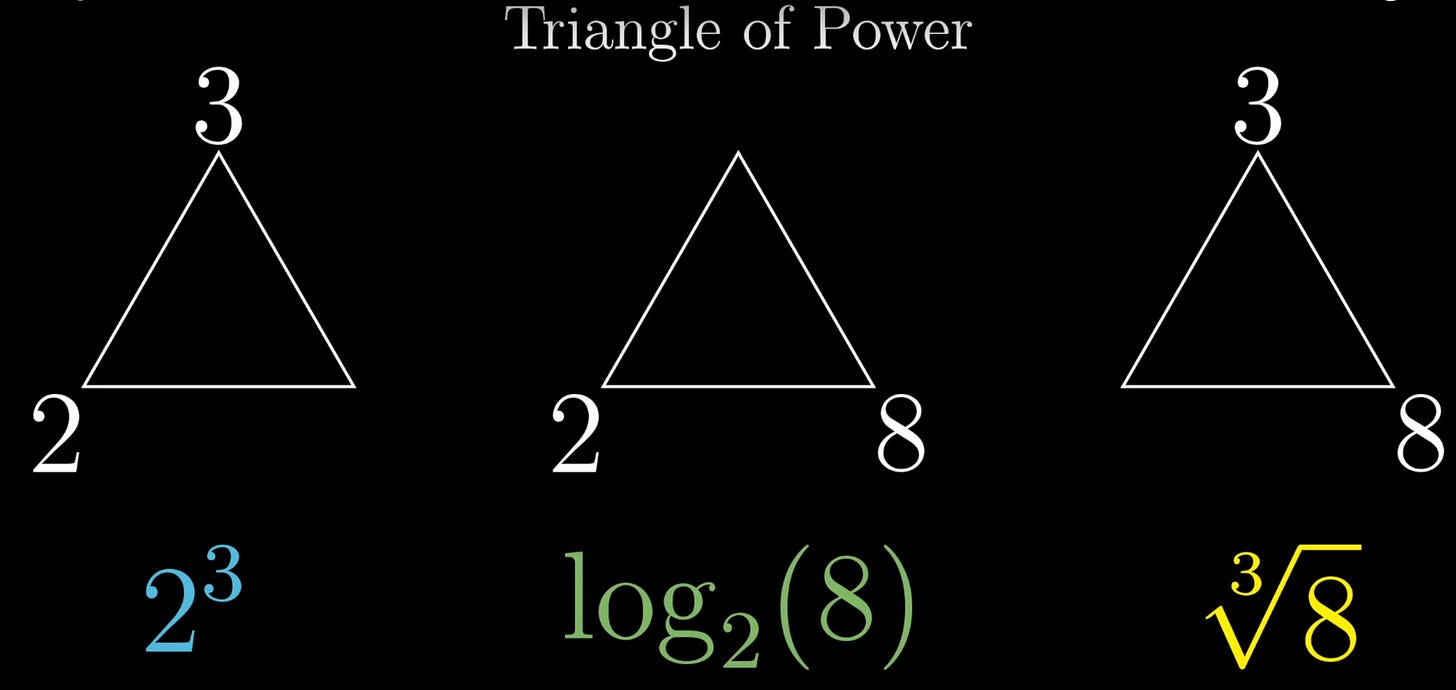
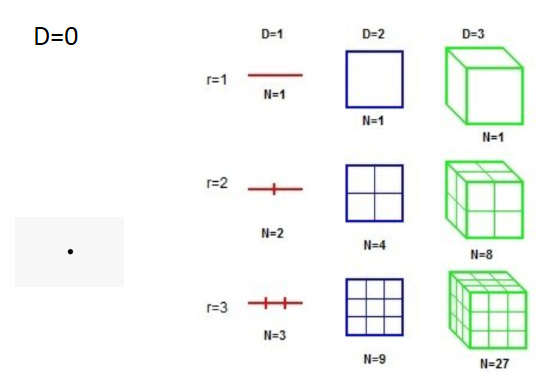

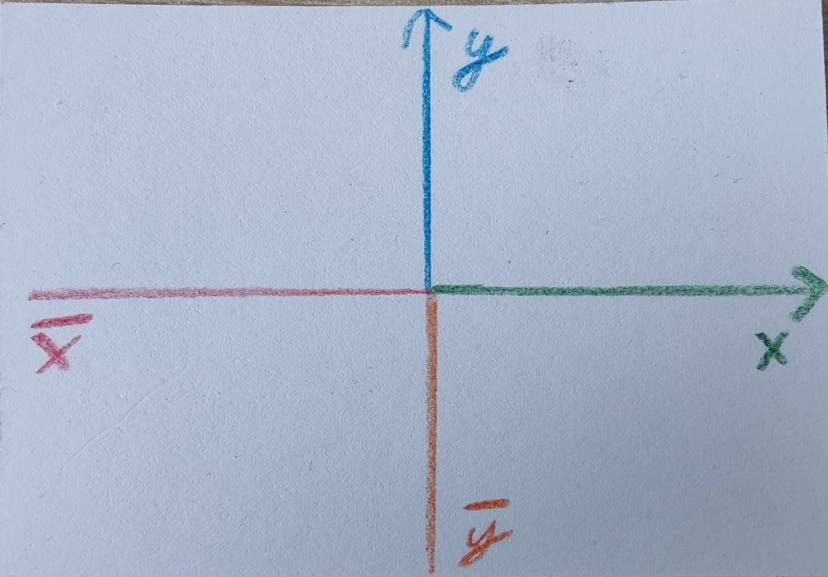
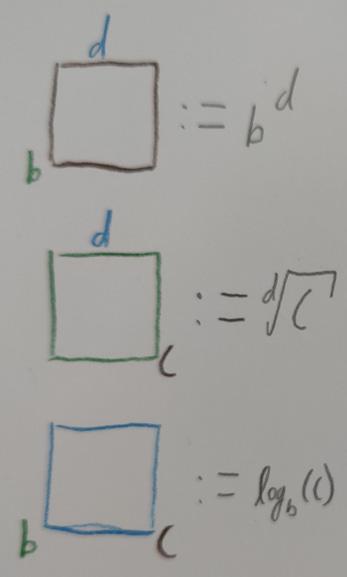
I see you keep building an optimal and geometrically-and-colored notation from scratch! It does feel more intuitive than the conventional one. I also remember watching 3b1b's video and it making a lot of sense to me.
Hey, this is clever!