Colored Number Squares for Enhanced Numeracy! Part 1
The Problem with Our Numbers being Only Almost Cool...
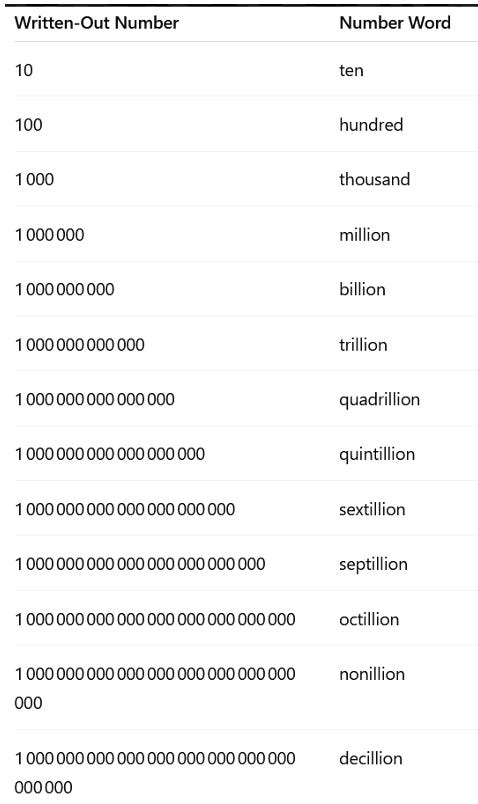
Let's take a look at how we express large numbers in English.
The Observed Pattern
These number words have some pleasing patterns.
”Thousand” and “Million” are a bit mysterious.
But after that, everything follows a prefix + illion pattern.
There is an ascending pattern of the usual Latin prefixes we are well familiar with.
Specifically (bi, tri, quad, quint, sext, sept, oct, non, dec)-pattern.

So every three digits, we seem to be counting one up in Latin numbers.
The Intuited Calculation
Wouldn’t it then not be most logical, that if we want to multiply or divide a set of large numbers, we could simply use those prefixes to instantly determine the new number word?
We would downright expect, that
1.
“a billion times a billion” is a quadrillion, as 2+2 equals 4.
2.
That a “billion times a trillion” a quintillion, as 2+3=5.
3.
Or that a “sextillion divided by a quadrillion” would be a billion, as 6-4=2.
4.
A “billion times a billion times a billion” would be a sextillion, as 2+2+2=6.
The Sad Truth
However, our number system is sadly a little twisted, hence the results are:
1. a quintilliion, which uses the prefix for 5
2. a sextillion, which uses the prefix for 6
3. a million, which does not use a prefix, but as the million comes before the billion, we could say that it maps the prefix for 1 instead
4. an octillion, which uses the prefix for 8
When we have two factors, the real product is always one stage than our intuition suggested. When we have three factors, it’s even two stages.
So the idea of “always increment what we expect by one” does not work well either, as we need to increment also whenever we add another factor.
Also in the third case where we divide, it’s one stage lower (rather than higher) than expected. How terribly confusing!
Why does this not work?!
The short answer is, the thousand ruins it for us.
What were we counting up, anyway?
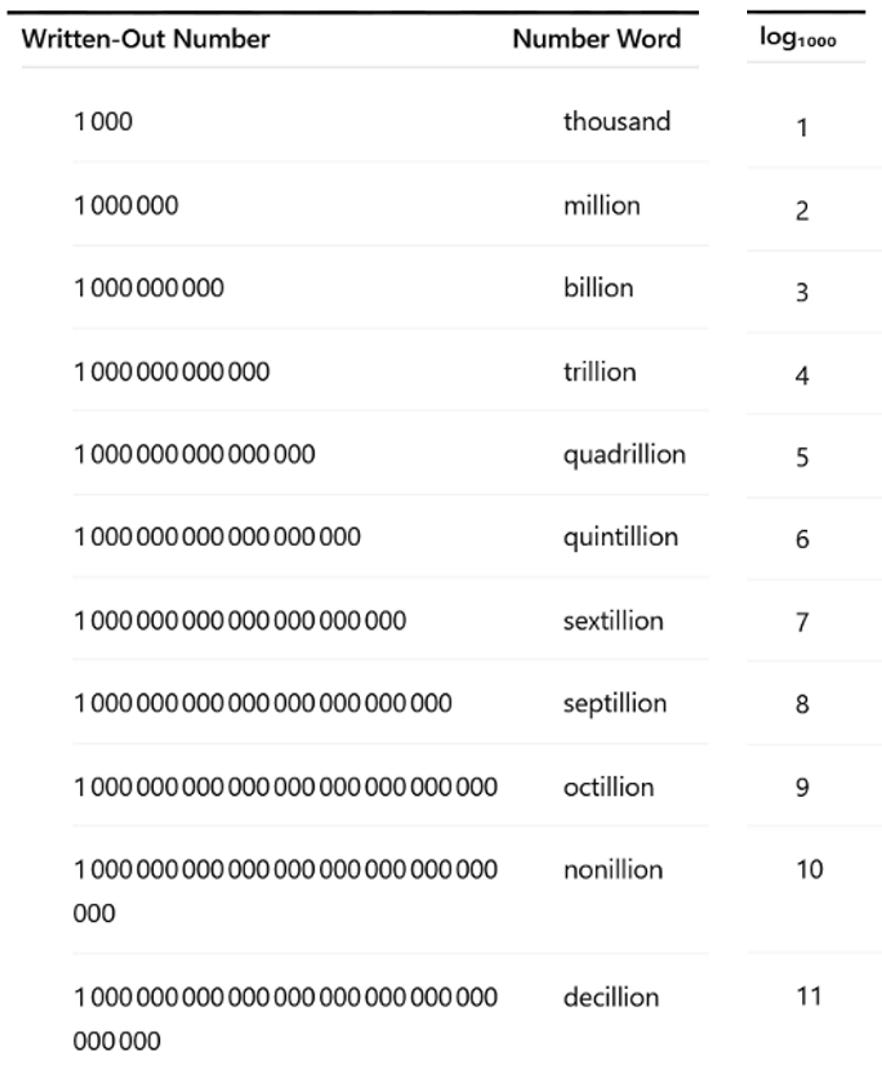
Every three digits we were adding a new number word. Or differently stated, whenever the 1000-logarithm of our number increments by 1.1
Trouble is, we are beginning this count at six zeroes, rather than at three zeroes.
Notice, how we can clearly see this terribly annoying offset here:
The Obvious (sadly infeasible) Solution
If we just skipped the number word for thousand or alternatively skipped the number word for million and went straight to the word billion for 10^6, the numbers would actually work exactly as intuition suggests.
However, I am sorry to say, that my ambitions of world conquest have so far been squashed, so I have little power to change the English language at this point.
Making people aware of this problem and how a simple change in convention could enhance the numeracy of every English speaker… could theoretically work.
But we don’t have time for that…
The Workaround: Colored Number Squares
First off, we get familiar with the color code I have introduced here.
Only the associations between primary colors and digits will be needed.
In words:
1 Red
2 Yellow
3 Green
4 Blue
5 Orange
6 Cyan
7 Purple
8 Brown
9 Gold
We apply this to numbers like so:
Vaguely Inspired, but Still Confused?
Then stay tuned for more posts this week on how we can use a colored square convention for enhanced numeracy and easier calculation. How we can extend it to negative powers and even replace the hateful French SI-prefixes with it!

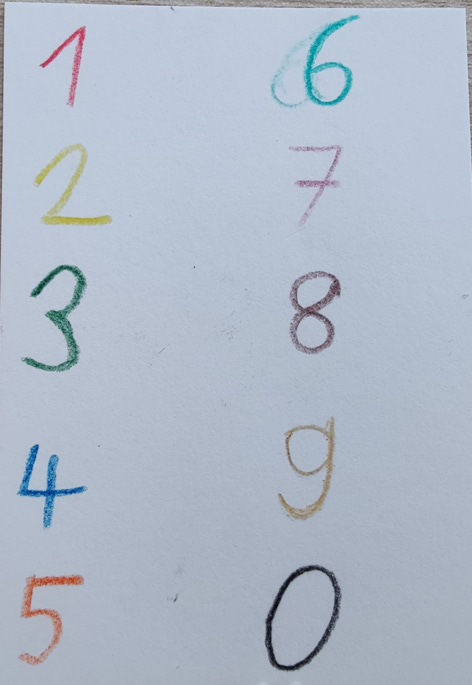

Why not simply use the prefixes for SI units? Tera, giga, mega, kilo, milli, micro, nano, pico, femto, etc. They are well known.
I’m interested to see where this goes.