Hypersquare: Linguistic Refactoring
Saphir-Whorf == True -> (betters Words -> smarter)
Note:
Simply accepting the new spoken syntax sets that I establish around the new argument-triple of (base, dimension, Content) can be done independently from using the hypersquare symbol. If you dislike adopting a new symbolic notation, this alone will be very useful on its own. But for enabling conceptual understanding, both conventions synergize extremely well with one another.
All the problems with Current Spoken Syntax
Exponentiation
Take the expression “b^d”.
When we speak it as ”b to the power of d” we regrettably mix output-parameter with the second argument parameter.
”exponenting b with d” could be another theoretical option, better would be “raising base b to the exponent d” avoiding some of those problems, but neither is perfect nor are they in use.
When discussing the operation of “exponentiation” what seems to be calculated is the abstract and dazzlingly overloaded idea of “power”.
The operation-name reflects the second argument, instead of what it calculates, which would be a far more logical and desirable property that even the hateful, problematic and soon to be forgotten legacy notation of sin(θ) spoken as ”sine theta”-notation manages to do by default, even if very badly.
What is Power, Anyway?
Now let’s look at the legacy output parameter of "power”:
Is 3^3=81 more powerful than 3^2=9?
Uhm… sure, that makes some sense based on vibes, but the language does not mesh with the geometrical ground truth the operation encodes, nor do we use the label of “power” in this context again. So we get fuzzy, conflicting vibes, instead of the clear, precise and uncompromising language that our soul craves to make sense of the world.1
Root Taking
Spoken as “taking the d-th root of C”. The parameter names of “degree”, “radicand” are not used.
From the spoken convention, one might easily assume that “root” as a label would refer to the first parameter d, which apparently is named the “radicand”. Indeed, this I assumed till just now myself.
Yet referring to the operation-parameter chart again, “root” refers to the output parameter now. I vaguely remember learning the term “degree” for the first argument a long time ago in school, but as the syntax is highly confused, I have conflated it2.
Let us then not further dwell on the mistakes of our forebears, and establish a powerful tradition of our own.
Logarithms
Instead of the recurrent whining, let’s at least say something nice about the most hated of operations…. at least the default parameter name of “base” is shared with exponentiation! In fact, it’s so good, that I decided to use the term myself!
And the output-parameter matches the operation-name here!
Back to the negatives though, and I bet you, that most people will not be familiar with the term “anti-logarithm”. Also, it’s very long and contains within itself the output parameter name! Bad.
When we say “taking the log of C", we often implicitly refer to base 10 or base e.
Sometimes we hear the clarifying phrase “taking the decadic log/the natural log of C/binary log” using words to encode the base-number.
It sort of makes sense, that we thereby define a more compacted unary-function, but it tends to add obfuscation and confusion, unless you’re already on friendly terms with the operation and its meaning. Another problem here is that the verb “taking” is already used for “taking the root”.
But let us then not further dwell on the mistakes of our forebears, and establish a powerful tradition of our own.
All the Solutions with New Spoken Syntax
Multiple Syntax Sets
I have experimented with different conventions and found it best, that there ought to be variations to emphasize different use cases, perspectives and different levels of required verbosity. And the option for terseness to improve cognitive performance and communication efficiency.
I will formalize this via a generative grammar eventually, but for now I list only the most important syntax sets as they sound out these three basic equations:
verbose
Usage Context:
Teaching or refamiliarizing yourself with simple geometrical hypersquare intuition.
b^d=C will be spoken as
"Conning base b into dimension d equals Content C".
"d-th root of C=b" will be spoken as:
"basing in dimenson d the Content C equals base b"
"log_b(C)=d" will be spoken as:
"dimming base b in the Content C equals dimension d"
terse
Usage Context: mental computation for beginners or at low-volume, context-implicit communication
b^d=C will be spoken as
"con base b into dimension d equals Content C"
For "d-th root of C=b” we say:
"base in dimenson d the Content C equals base b"
So for log_b(C)=d we say
"dim base b in the Content C equals dimension d"
ultra-terse
Usage Context: high performance or high volume mental computation, also high volume communication, if meaning is solidly established via context
Notes:
Instead of "equals", we use "is", gets rid off redundant init-verb and goes fully monosyllabic. Prepositions? No time!3
b^d=C will be spoken as
"base b dimension d is Con C"
For "d-th root of C=b” we say:
"dim d Con C is base b"
So for log_b(C)=d we say
"base b Con C is dim d"
ultra-terse with abstract parameters:
Usage Context: for memorizing or quickly recalling various laws with minimal overhead
Notes: Instead of "equals", we use "is", gets rid off redundant variable names and init-verb and goes fully monosyllabic.
b^d=C will be spoken as
"base dim is Con". or even "base-dim Con"
For "d-th root of C"=b we say:
"dimCon is base" or even "dim-Con base"
So for log_b(C)=d we say
"base Con is dim" or even "base-Con dim"
Fancy Geometric Ultradimensional Child Play Metaphor (Preview):
Meta Note:
Properly explaining and illustrating what this all means and why it's a great way to enable intuitive understanding of the operations, will involve a lot more groundwork in future posts.
Usage Context:
Educational for conveying a deep, hyperdimensional understanding.
Footnote: Will also be useful once we generalize the operation-triple for orthoplexes and simplexes as well and will potentially include fractal dimensions
Note:
Here the initial starting verb no longer redundantly encode the operation name, but rather encodes what an ultrageometric child will do, as it executes the various operations by interacting variously with unary units, hypersquares and hyperdimensional educational toys, tools and machines. "Equals" will be replaced with the observed outcome of that process.
b^d=C will be spoken as
"taking base b into dimension d gets Content C".
For "d-th root of C=b” we say:
"placing into dimenson d the Content C builds base b"
So for log_b(C)=d we say
"noting base b in the Content C shows dimension d"
at least I suspect myself to be in good company within that misfortune
Why does pasting a video-link into a footnote embed it above the footnote?!




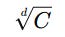



Surely sin(θ) is spoken as "sine theta"?