Write Math Fast: Unary Addition/Subtraction
Back to those lovely numbers children!
What’s this About
I’m sure you’ve read my “Unary Addition”-article full of fascination and childlike wonder. And then were puzzled about all these brilliant applications I promised would come soon. Promised…. in May. Oops
I was a bit sick of doing all this finnicky math stuff. But now the work is sped up a lot, by my shiny new Galaxy Tab S7. So here we go!
Some Programming First
Let’s look at a little programming example of a loop.
Note that the =-sign means something fundamentally different than in mathematics. It denotes an assignment, rather than an equality.
The notation of:
a := 5
comes closest and is commonly used for definitions, it can be interpreted as
”a is defined as (a variable with the value of) 5”.
The distinction between stating an equality and an assignment might seem a little unimportant, from a mathematical perspective where we don’t reassign variables.1
The expression “i++” is syntactic sugar for:
i = i + 12
This is faster to type and uses fewer characters.
The situation where you increment or decrement by one comes up all the time, so this shorthand makes code faster to type and read, once you’re familiar with it.
This reassignment uses a form of unary shorthand addition.
The same way you might be familiar in some versions of vertical addition, where we denote a carryover in a similar quick fashion:
Of course, if you’re familiar with my unary basics notation you can do more than just easily increment or decrement by one in such situations.

We often have complex expressions, where we have yet another units-place value that needs adding. To cut down on the number of terms, I introduce the following conventions:
Some examples
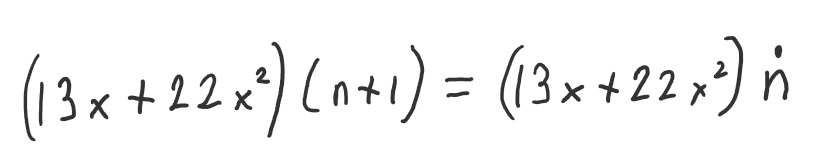
The Linguistics of It
Speaking out a formula, it’s helpful if you can name the symbol you’re seeing, rather than needing to translate it into others.
So when you see a n with a dot above, you could simply call that out as “n dot”, rather “n plus one”. Similarly the with the line above could be spoken “n line” instead of “n plus 2”. For the negative values, it’d be “n circle” or “n circ” over “n minus one” and “n circ line” over “n minus two”.
Even if the mathematical expression of “22x^2 * (n+1)” is not in this format, you can also verbally shorten it to just “twentytwo x squared times n dot” compared to the much longer “twentytwo x squared times open parenthesis n plus one close parenthesis”.
It might seem a bit complicated and redundant to invent this an extra set of number words.
By using different number words, we can easily separate the different number-spaces by context. You can never confuse “n one”, which is n with a subscript of one with “n dot” which is just shortened “n plus one”.
We can even combine both without adding any confusion:
Applying to Sequences
This convention also shines when applied to subscripts, as the ideas of “successor” and “predecssor” within a sequence can be far more concisely expressed.
Take these recursive sequences:
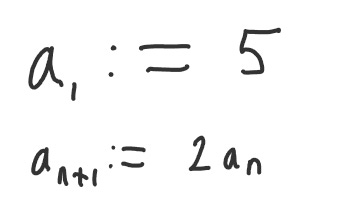
Sequences should be Written Differently!
But in general I find the “n+1”-convention in the index of a definition to always be very mentally taxing and inviting mistakes. Usually I want to know a specific value like n_5. But I can’t just mentally plug 5 into the second expression here, but need to first deal with the offset.
So I plug in 5 into the second line, need to calc out that this gives me actually the value for a_6, then need to remember that I actually need to set n to 4. Unary offsets can be extremely confusing, if they are placed like this. It’s very simple to forget, that n is not “the value that you are interested in looking up”. Even writing exactly what has to go on in my head, when I want to calculate a specific entry, I get myself easily confused. It’s so bad, I refuse to reread any of this part for editing :)
Somehow this kind of “subscript-variable +1” definition was used all the time in my Computer Science course.3
Well, I much prefer having “n” be the thing that I’m trying to look up, which you can define like so:
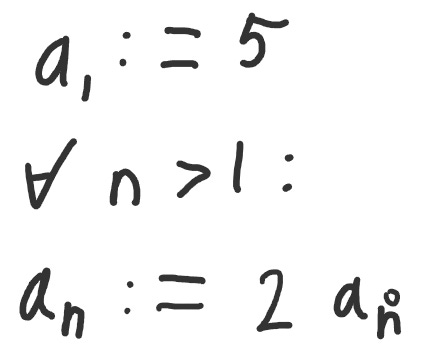
That I know of. It might be worth stealing this convention for expressing math more cleanly and concisely, but I’m not sure how to best implement it yet. Lots of programming conventions are sorely missing in math I find.
also the related i-- is shorthand for “i = i -1”
The entire field is full of brilliant ideas, but also cursed with highly annoying offset-problems like this or those that are introduced by zero-based counting. When a CS-grad tells you that zero-based counting is superior, it is because some early work in storage addressing saddled us with nigh unkillable legacy notation, that we’ve collectively gotten Stockholm syndrome from.


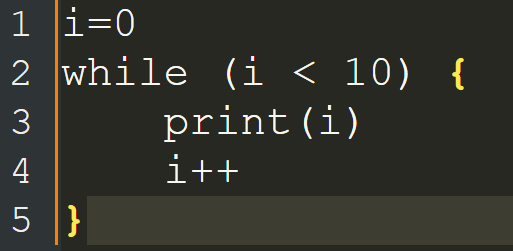
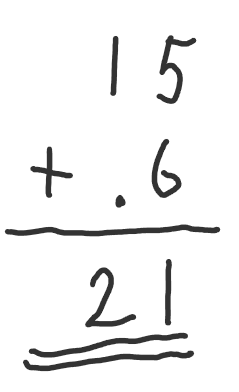
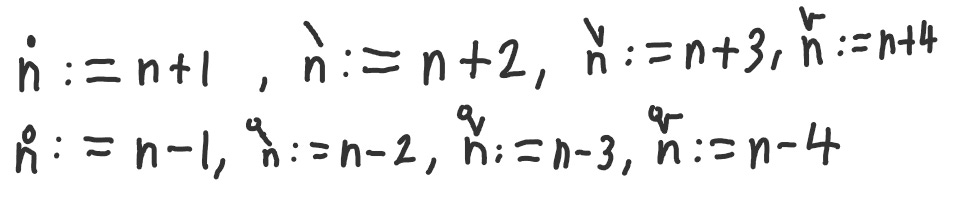
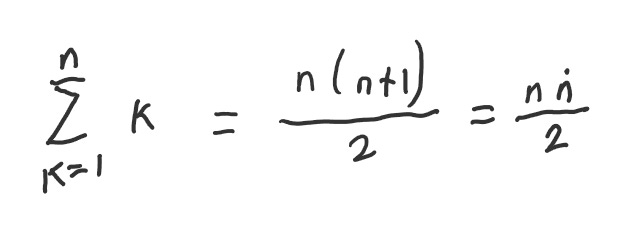

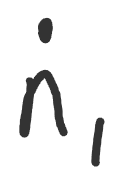
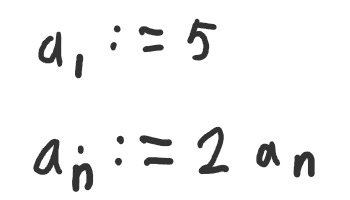
This would save a lot of time!